PHSP Súradnice na oblohe

Miroslav Znášik, Hvezdáreň v Žiline, Horný Val 20/41, 010 01 Žilina

Pre bežného pozemšťana je obloha dutou guľou, ktorej polovica je zakrytá zdanlivým horizontom. Tak ju vnímame svojou skúsenosťou. Vnímavejší, pozorujúc Mesiac a Slnko zdanlivo väčšie pri obzore, ako vysoko nad ním, sú ochotní pripustiť jej deformáciu do tvaru „klenby“. Astronomicky vzdelaný pozorovateľ vie, že ako všetko ostatné je i tento pohľad iba prvým priblížením, že vplyvom mnohých skreslení sú polohy telies na nebeskom firnamente iba väčšou, či menšou ilúziou. Ako hlboko musíme skúmať všetky tieto reálne fyzikálne vplyvy, optické klamy a nakoniec i vlastnosti seba samého, aby sme sa dostali do reality pozorovateľskej praxe? Túto otázku sa pokúsime zodpovedať v nasledujúcom texte.

Obr.1. Pohľad na oblohu je projekciou rôzne vzdialených objektov na nebeskú sféru. Najväščou ilúziou sú tak súhvezdia, ktoré spájajú rôzne vzdialené objekty do mýtických kreatúr. Hviezdokopa M13 v súhvezdí Her je oveľa ďalej ako ostatné hviezdy súhvezdia.

1. Trochu histórie

Najstaršiu históriu – popísanie oblohy a objektov na nej našimi dávnymi predkami – vynecháme. Siaha totiž veľmi ďaleko a doposiaľ nie je presne zrekonštruovaná. Od jednoduchého popisu oblohy musíme odlíšiť snahu o kvantitatívne presné popísanie polôh nebeských telies, ktorá je charakteristická pre helénistické obdobie antiky. Obloha podľa Thálesa z Milétu mala údajne tvar pologule nad vtedy ešte plochou Zemou, plávajúcou na Oceáne (1). Jeho nasledovník, Anaximandros, popisuje prvýkrát oblohu ako dutú guľu, v ktorej rovnako vzdialená od všetkého, pláva uprostred Zem v tvare bubna. Neskôr Pytagorejci preukázali guľatosť Zeme; najskôr v smere severojužnom (z viditeľnosti hviezdy Canopus pri plavbách v Stredozemnom mori) a po nich Aristoteles skutočnú guľatosť Zeme z tvaru tieňa Zeme pri zatmeniach Mesiaca. Sféra stálic sa tak udomácnila v modeloch Vesmíru a pretrvala až do novoveku. Aj M. Koperník predpokladal za planétami krúžiacimi okolo Slnka všade rovnako vzdialenú „stellarum fixarum sphaera immobilis“. Prvou vedeckou teóriou, ktorá túto krištáľovú sféru zrušila, bol objav vlastného pohybu hviezd (u hviezd Arcturus, Sírius a Aldebaran) E. Halleym v r.1718. Až neskoršie pozorovania W. Herschella, R. Kapteyna a H. Oorta definitívne potvrdili špirálnu štruktúru Galaxie a kvázi hierarchickú (priestorovú) štruktúru Vesmíru. Pre naše praktické potreby sférickej astronómie však stále považujeme všetky hviezdy za rovnako (nekonečne) vzdialené.

2. Horizontálna (obzorníková ) sústava súradníc

V každej súradnicovej sústave môžeme definovať významné roviny a smery, ktoré charakterizujú sústavu jednoznačne a nezameniteľne v porovnaní s inou súradnicovou sústavou, rovnocenne popisujúcou polohu telies na oblohe. V horizontálnej sústave sú to rovina skutočného horizontu a smer ku južnému bodu miestneho poludníka – meridiánu. Rovina horizontu je daná smerom tiaže v mieste pozorovateľa na povrchu Zeme. Rovina kolmá na smer tiaže, prechádzajúca pozorovateľom (okom pozorovateľa) je rovina skutočného horizontu. V ďalšom texte budeme túto rovinu volať rovinou horizontu, prívlastok „skutočného“ vynecháme. Nebeskú sféru pretína táto rovina v hlavnej kružnici na sfére, ktorú voláme skutočným horizontom. Prísne vzaté, je horizont ideálnou krivkou, ktorá reálne neexistuje. Asi najbližšie by k nej bola rovina obzoru pre pozorovateľa v nulovej výške nad pokojnou hladinou oceánu. Na súši, s výnimkou veľkých a rovných oblastí bez vegetácie, vidíme v praxi obzor – miesto, kde sa spája „nebo“ so vzdialenými objektami nad horizontom. V námornej praxi sa uvažuje o výške pozorovateľa nad oceánom, ktorá posúva obzor pod horizont (zakrivenie Zeme je asi také, že z výšky (oka) 5 m vidíme do vzdialenosti 8 km). Pri meraniach výšok hviezd klasickým sextantom sa namerané hodnoty korigujú (empirickým) členom: K(´) je hĺbka horizontu v minútach, Ah(m) je výška v metroch: (2)

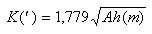
Od zvoleného bodu – južného bodu skutočného horizontu – v kladnom smere meriame v rovine horizontu astronomický azimut. Rovnakým smerom meriame i topografický azimut, ale od severného bodu horizontu. Južný bod horizontu je miesto, v ktorom horizont pretína meridián – miestny poludník pozorovateľa. Ten spája hlavnou kružnicou pozorovateľa, severný svetový pól a zenit. Kolmo ku rovine horizontu, kladne ku zenitu - nadhlavníku, meriame druhý uhol telesa – výšku nad horizontom. Pre telesá pod horizontom je výška záporná (napr. pozorovanie v horách smerom do hlbokej doliny), pre smer do zenitu je výška 90°. Doplnkovým uhlom ku výške je zenitová vzdialenosť z.

3. Rovníková sústava súradníc

Hlavnou rovinou rovníkovej sústavy je rovina nebeského rovníka. Na oblohe si ho môžeme predstaviť ako hlavnú kružnicu, ktorá vzniká prienikom roviny pozemského rovníka s nebeskou sférou. Svetový rovník pre pozorovateľa na ľubovoľnom mieste Zeme (s výnimkou pólov) pretína rovinu horizontu vo východnom bode horizontu E, kde vychádza nad horizont a v západnom bode horizontu W, kde zapadá. Kolmo ku rovine svetového rovníka, smerom ku severnému svetovému pólu, sa kladne a smerom k južnému svetovému pólu sa záporne meria deklinácia hviezdy (obdoba výšky). Hlavnú kružnicu, prechádzajúcu pozorovateľom, severným svetovým pólom a hviezdou, preto voláme deklinačnou kružnicou. Podľa toho, ako zvolíme v rovine svetového rovníka významný smer, môžeme rovníkovú sústavu definovať dvoma spôsobmi:

1. ak zvoleným smerom je priesečník svetového rovníka a miestneho poludníka (obdoba južného bodu horizontu na svetovom rovníku), meriame od tohto bodu v kladnom smere po svetovom rovníku hodinový uhol telesa t
2. ak zvoleným smerom v rovine svetového rovníka je jarný bod – priesečník svetového rovníka s rovinou ekliptiky – meriame v zápornom smere rektascenziu telesa α

Použitie sústav a) – obvykle nazývanej rovníkovými súradnicami prvého druhu, alebo b) – obvykle pomenovanou rovníkovými súradnicami druhého druhu, definuje naša aktuálna potreba. Kým pre hviezdne mapy a atlasy je výhodnejšie zobrazovanie oblohy v druhej sústave (α, δ), ktorá sa časom (ak zanedbáme vlastný pohyb hviezd a dlhodobú zmenu orientácie rotačnej osi Zeme) nemení, pre pozorovateľskú prax je významná prvá sústava.

Teleso v kulminácii nad južným bodom horizontu (hovoríme o hornej kulminácii) má v okamihu prechodu poludníkom hodinový uhol rovný nule!

Najmä ďalekohľady na paralaktickej montáži možno jednoducho nastaviť pomocou hodinového uhla a deklinácie na zvolený objekt.

4. Hviezdy a slnečný čas

Obe rovníkové sústavy spája súvislosť s hviezdnym časom. Hviezdy deň má 86 164,556 sekúnd a predstavuje čas otočenia Zeme okolo osi voči hviezdam. Na stredný slnečný čas, predstavujúci dobu rotácie Zeme voči „strednému“ Slnku ho prepočítame jednoducho: jeden tropický rok (čas obehu Zeme okolo Slnka) je práve o jeden hviezdny deň dlhší, ako rok vyjadrený v stredných slnečných dňoch. Z tohto pomeru možno definovať prepočet časov hviezdneho t* a slnečného času t_S vzťahom :

t* = 1,0027379093 t_S

Súradnice t i α sú preto vyjadrené v časovej miere v jednotkách hviezdneho času.

Čas je všeobecne hodinovým uhlom časomerného telesa (alebo bodu).

V dôsledku nerovnomerného pohybu Zeme okolo Slnka musíme okrem skutočného stredu Slnka (tzv. pravé Slnko) zaviesť (prvé) stredné Slnko – fiktívne teleso, ktoré sa rovnomernou rýchlosťou pohybuje po ekliptike tak, že s pravým Slnkom sa stretáva v okamihoch prechodu perihéliom. Vplyvom sklonu ekliptiky ku hlavnej rovine sústavy – svetovému rovníku – musíme definovať ďalšie (druhé) stredné Slnko, pohybujúce sa zdanlivo po rovníku tak, že sa s prvým stredným Slnkom stretá v dni rovnodenností. Rozdielom rektascenzie pravého Slnka a druhého stredného slnka je časová rovnica, ktorú poznáme v grafickom vyjadrení ako analému.

Hodinový uhol druhého stredného Slnka, definitoricky zväčšený o 12 hodín (deň začína od 1.1.1925 od polnoci) je stredný slnečný čas.

Tento čas pre pozorovateľa na nultom (Greenwichskom) poludníku je svetovým časom UT. Zem je dohodou rozdelená na časové pásma, v ktorých sa používa jednotný pásmový čas. U nás používame pásmový posun + 1 hod, t.j. miestny čas 15° východnej zemepisnej dĺžky (žiaľ, v zákonom stanovenom období je posun 2 hodiny a používame tzv. „letný“ čas). Pokiaľ sa pozorovateľ nachádza na inom poludníku, ako je pásmový, pozoruje pravé Slnko v občianskom pásmovom čase t_P v hodinovom uhle

t*=S₀ + 1,0027379093 (t_P - 1) + λ - α

kde λ je zemepisná dĺžka pozorovateľa (kladná východne od Greenwicha) α a je rektascenzia pravého Slnka. Hodnota S ₀ je hodinový uhol jarného bodu na Greenwichskom poludníku a je tabelovaná pre polnoc UT v Astronomickej ročenke (3). Denne sa pravidelne zväčšuje o rozdiel medzi stredným slnečným a hviezdym dňom (236,55 sek) a o oscilujúcu malú hodnotu (nutáciu v rektascenzii, najviac ±1,07 sekundy), ktorá je dôsledkom zložitého pohybu rotačnej osi Zeme spôsobého príťažlivosťou Mesiaca. Prvé tri členy výrazu na pravej strane rovnice možno vyjadriť ako

t* = S₀ + 1,0027379093 ( t_P – 1 ) + λ

a nazvať ho miestnym hviezdym časom „s“; hodinovým uhlom jarného bodu pre pozorovateľa v zemepisnej dĺžke λ v občianskom čase pozorovania t_P. Porovnaním oboch rovníc zistíme ľahko, že súčet rektascenzie hviezdy a jej hodinového uhla je miestny hviezdny čas. Inak povedané, rektascenzia kulminujúcej hviezdy (s nulovým hodinovým uhlom) určuje miestny hviezdy čas. Ak pozorovateľovi kulminuje hviezda s rektascenziou a, je práve a hodín miestneho hviezdneho času.

Túto skutočnosť môžeme využiť v pozorovateľskej praxi pri vytýčení miestneho poludníka. Ak máme zdroj presného občianskeho času (rádiom riadené hodiny) a poznáme (z mapy) presné súradnice pozorovateľa, môžeme pre hviezdu so známou rektascenziou vypočítať okamih jej prechodu miestnym poludníkom. V tomto čase je hviezda s deklináciou menšou ako je zemepisná šírka pozorovateľa presne nad južným bodom jeho horizontu.

5. Skutočné a zdanlivé polohy telies na oblohe

Už v staroveku boli nebeské telesá rozdelené do dvoch tried – stálic a obežníc. Kým stálice vykonávali svoj pravidelný denný pohyb okolo Zeme, obežnice sa po zložitých dráhach, raz priamo (t.j. prográdne, s rastúcou rektascenziou, či dĺžkou), inokedy opačne (retrográdne, proti smeru zdanlivého pohybu Slnka voči hviezdam) pohybovali medzi súhvezdia. V ďalšej časti si postupne ukážeme, ako sa líšia skutočné polohy a polohy zdanlivé - pre pozorovateľa na zložito sa pohybujúcej Zeme. V astronomickej praxi hovoríme o redukčných veličinách, ktoré korigujú ideálne polohy na skutočné, pozorované. Principiálne ich môžeme rozdeliť podľa vplyvu na polohy veľmi vzdialených telies – hviezd – a relatívne blízkych objektov slnečnej sústavy. Pri korekciách definujeme vždy rozdiel skutočnej (pozorovanej) a teoretickej (vypočítanej, predpovedanej) hodnoty. Jednotlivo ich môžeme charakterizovať a popísať nasledovne (4):

Astronomická refrakcia: Posúva telesá do zenitu pozorovateľa. Azimut telesa sa pritom nemení. Pre zenitové vzdialenosti do 70° možno refrakciu vyjadriť približným vzťahom

z - z₀ = k * tan(z₀)

kde konštanta refrakcie k je funkciou teploty a tlaku vzduchu ( v „normálnych“ podmienkach t = 20°C, 1013 hPa je k =̃ 1´). Veľmi rýchlo sa mení v malých výškach nad horizontom, kde pre prax viac vyhovujú refrakčné tabuľky. Na horizonte dosahuje najvyššiu hodnotu - až 35´! V malých výškach sa významne uplatňuje aj vplyv vlnovej dĺžky svetla,v ktorej pozorovania vykonávame; u hviezd vzniká refrakčné spektrum. Okraje Slnka, Mesiaca a planét nízko nad obzorom sú charakteristicky sfarbené. Ich horný okraj má tendenciu sfarbovať sa do modra a spodný do červena. Zriedkavým úkazom nízko nad obzorom je tzv. „zelený lúč“. Vzniká kombináciou „modrého“ a „červeného“ refrakčného obrazu Slnka pri západe (alebo východe), ktorý vidíme zelený s ohľadom na vlastnosti oka a atmosféry. V rovníkových súradniciach možno vplyv refrakcie na polohu telesa vyjadriť pomocou „airless“ súradníc (α₀, δ₀) resp. (t₀, δ₀) a paralaktického uhla η (uhol pól – hviezda – zenit v nautickom trojuholníku, v Prílohe 1.) zo zenitovej vzdialenosti z₀ (bez vplyvu atmosféry):

z = z₀ + k tan(z₀)
t -t₀´ = -k tan(z) sec(δ) sin(η)
&delta - δ₀ = k tan(z) cos(η)
α - α₀ = k tan(z) sec(δ) sin(η)

Vo výraze pre zmenu rektascenzie a hodinového uhla musíme uhlovú mieru nakoniec previesť na časovú.

Obr.2. Nízko nad obzorom zmení diferenciálna refrakcia tvar Slnka a Mesiaca (na obrázku pri prstencovom zarmení 31. 5. 2003) na nepoznanie.

Astronomická aberácia: Vplyvom pohybu pozorovateľa na Zemi je každý objekt na oblohe posunutý smerom ku apexu jeho pohybu; v prípade pohybu okolo Slnka ide o bod na ekliptike, ktorý je 90° „za“ Slnkom, má dĺžku o 90°menšiu. Aberačná elipsa má veľkú poloos pre všetky hviezdy rovnako veľkú, s hodnotou rovnou aberačnej konštante A = 20,5“. Malá poloos sa mení s ekliptikálnou šírkou β (obdoba deklinácie v ekliptikálnej sústave) a má hodnotu A sin β. Hovoríme potom o ročnej aberácii. Objavil ju J. Bradley v r. 1727 z pozorovaní hviezdy Etamin pri hľadaní paralaxy hviezd. Ak zavedieme konštanty C, D, c, d, c´ a d´, môžeme pre zmenu polohy hviezdy vplyvom aberácie písať:

(α - α₀)^S = C*c + D*d
(δ - δ₀)" = C*c' + D*d'
C = - A cos ε cos λ_S
D = - A sin λ_S
c = (1/15) cos α sec δ
d = (1/15) sinα sec δ
c' = tan ε cos δ - sin α sin δ
d' = cos α sin δ

kde C a D sú tzv. Besselove denné čísla, rovnaké pre rovnaký časový okamih pre všetky hviezdy. Hodnoty c, d, c´ a d´ sú definované polohou hviezd. Horný index s znamená v prvej rovnici i v nasledujúcich rovniciach vždy údaj v časovej miere (sekundách hviezdneho času).

Ďalšou možnosťou je definovať tzv. „nezávislé denné čísla“ H, h a i pomocou vzťahov:
(a):h* cosH = - A*sin λ_S
(b):h*sinH = - A*cos ε * cosλ_S
(c):i = -A.sin ε * cosλ_S

kde λ_S je ekliptikálna dĺžka Slnka a určiť opravy o aberáciu pomocou vzťahov:

(α - α₀)^S = (1/15)h*sin(α + H)secδ
(δ - δ₀)^" = i*cosδ + h*cos(H + α) sin δ

Denná aberácia je spôsobená pohybom pozorovateľa na rotujúcej Zemi. Apex tohto pohybu leží na východnom bode horizontu a tým smerom sú posunuté všetky polohy telies na oblohe. Denná aberácia je oveľa menšia a jej konštanta má hodnotu iba 0,32“.cos φ´, kde φ´ je geocentrická šírka pozorovateľa (blízka zemepisnej). Túto redukciu s ohľadom na veľkosť (u nás do 0,22“) používame iba vo výnimočných prípadoch.

Ročná paralaxa: Vzniká pohybom Zeme okolo Slnka. Voči polohám mysleného pozorovateľa zo stredu Slnka sa polohy hviezd počas obehu Zeme posúvajú po oblohe po veľmi malej paralaktickej elipse, smerom k Slnku. Jej veľká poloos má rozmer χ“ a malá poloos hodnotu χ“ sin β. Pritom je χ“ paralaxa v oblúkových sekundách a b je ekliptikálna šírka hviezdy – obdoba deklinácie v sústave ekliptikálnych súradníc (meraná po šírkovej kružnici od ekliptiky ku jej pólu kladne na sever a záporne na juh; ekliptikálna dĺžka λ rastie v smere rektascenzie a meria sa po ekliptike od jarného bodu). Zmenu heliocentrických rovníkových súradníc na geocentrické (s pozorovateľom v strede Zeme) vplyvom paralaxy možno vyjadriť:

(α - α₀)^S = C₁c₁ + D₁d₁
(δ - δ₀)" = C₁c₁' + D₁d₁'
C₁ = R cosε sinλ_S
c₁ = (1/15)π cosα secδ
d₁ = (1/15)π sinα secδ
D₁ = -R cosλ_S
c₁' = π(tanε cosδ - sinα sinδ)
d₁' = π cosα sinδ

kde C₁ a D₁ nezávisia od hviezdy a sú pre všetky hviezdy v danom okamihu rovnaké a parametre c₁, d₁, c₁´ a d₁´ zase nezávisia od času a sú iba funkciou heliocentrických (stredných) polôh hviezd a ich paralaxy. R vo vzťahoch predstavuje sprievodič Zem – Slnko a λ_S je ekliptikálna dĺžka Slnka. Najväčšie paralaxy majú hodnoty iba do 0,7“.

Inou možnosťou je korekcie vyjadriť pomocou pravouhlých rovníkových súradníc Slnka, kde os X vedie do jarného bodu, os Y kolmo na ňu v rovine rovníka v smere (zdanlivého) pohybu Slnka medzi hviezdami a os Z kolmo na rovinu rovníka, do severného svetového pólu. Potom platí:

X = R cosλ_S
Y = R sinλ_S cosε
Z = R sinλ_S sinε
(α - α₀)^S = (1/15)π" (Y cosα - Xsinα) secδ
(δ - δ₀)" = π" (Z cosδ - X cosαsinδ - Ysinαsinδ)

Precesia a nutácia: Precesia je dlhoperiodický pohyb rotačnej osi Zeme okolo pólu ekliptiky, v kladnom smere. Jej príčiny sú v sklone rotačnej osi Zeme voči rovine ekliptiky, sploštení zemského telesa vytvárajúceho rovníkovú „výduť“ a príťažlivosti Mesiaca, Slnka a planét. Nutácia je krátkoperiodická zložka relatívneho pohybu rotačnej osi Zeme, ktorá dopĺňa precesný pohyb jedným smerom kývavými pohybmi v perióde 18,61 roka. Súvisí s pôsobením Mesiaca a sklonom jeho dráhy ku rovine ekliptiky.
Ak definujeme pravý jarný bod (priesečník rovníka a ekliptiky) ako bod podliehajúci precesii aj nutácii, môžeme stredný jarný bod definovať ako jarný bod nepodliehajúci nutácii, ktorého poloha sa mení iba dlhodobým precesným pohybom.

Rozdiel v rektascenzii pravého a stredného jarného bodu voláme nutáciou v rektascenzii.

V ekliptikálnej sústave súradníc λ, β sú definované nutácia v dľžke Δψ a nutácia v sklone Δε; sú to vždy malé uhly, ktoré možno premietnúť z roviny ekliptiky do sústavy rovníkových súradníc tak, že korigujú pozorované hodnoty rektascenzie a deklinácie hviezd v priebehu 18,61-ročnej periódy. Oba sú definované konvergentnými radmi goniometrických funkcií s klesajúcimi amplitúdami a argumentmi rastúcich násobkov hodnôt stredných anomálií Slnka a Mesiaca a dĺžok pericentra dráhy Mesiaca. Ak zanedbáme členy s malými amplitúdami, platí pre nutáciu v dĺžke a sklone približne:

Δψ = -17.234" sinΩ_M + ......
Δε = 9.210" cosΩ_M + .....

Nutácia mení v ekliptikálnych súradniciach iba ekliptikálnu dĺžku, šírka sa nemení. V rovníkových súradniciach môžeme podľa polohy hviezdy voči rovine svetového rovníka a sklonu ekliptiky k rovníku e vyjadriť zmenu súradníc nutáciou podľa vzťahov:

(α - α₀)^S = (cosε + sinε*tanα*tanδ) Δψ - cos α*tan*Δε
(δ - δ₀)" = cosα*sinε*Δψ + sinα*Δε

Ak sme v časti o čase suverénne hovorili o „jarnom“ bode, teraz už môžeme striktne rozlíšiť pravý jarný bod, ktorý podlieha precesii a nutácii a stredný jarný bod, ktorý predstavuje pravú polohu pre určitý presne stanovený čas – ekvinokcium. V súčasnosti sa používajú ekvinokciá odvodené od štandardnej juliánskej epochy J2000.0 = 2451545 po 365,25 dňa, ktoré pre konkrétny dátum JD (počet dní od poludnia 1.1.4713 p.n.l.) určíme pomocou vzťahu:

J [2000,0 + (JD - 2451545,0)/365,25]

Rozdiel rektascenzie pravého a stredného jarného bodu potom môžeme nazvať nutáciou v rektascenzii (tiež sa jej hovorí „rovnica ekvinokcii“) a vyjadriť (v časových sekundách hviezdneho času) formulou:

α_v^S = (1/15)*Δψ*cosε

Precesiou sa mení (plynule) poloha severného svetového pólu po kružnici so stredom v póle ekliptiky. Jej rýchlosť n je iba funkciou sklonu rovníka ku ekliptike ε, dynamického sploštenia Zeme a elementov dráhy Zeme a Mesiaca:

n = (5490.66" - (0.0364T_S))*sinε*cosε

Oveľa pomalšie sa tiež mení poloha pólu ekliptiky; preto sa pre každé ekvinokcium určuje vždy nová hodnoty konštanty precesie - n. Ak je m (precesia v rektascenzii) definované ako ročný pohyb jarného bodu po svetovom rovníku a n už spomenutá ročná zmena polohy svetového pólu, môžeme pre krátkodobé zmeny súradníc písať

p_α = m + n*sinα*tanδ
p_δ = n*cosα

a definovať ich ako ročné zmeny rektascenzie a deklinácie. Jej hodnoty sú udávané v ročenkách (súčasné hodnoty predstavujú: m = 46,123“= 3,07846 sek. a n = 20,0435“ = 1,33624 sek). Ide pritom o zmeny, vyplývajúce z inej polohy súradnicovej sústavy. Precesiu nájdeme i v lepších hviezdnych atlasoch; hlavne v blízkosti severného svetového pólu je zreteľné, že sieť hraníc súhvezdí má iný stred ako dnešný pól; zodpovedá polohe pólu v r. 1928, kedy boli hranice súhvezdí na podnet IAU kodifikované.

Vlastný pohyb hviezd: Pohyb Slnka a ostatných hviezd okolo stredu Galaxie sa pre pozorovateľa v strede Slnka prejaví posunom hviezd oproti predchádzajúcim polohám. Hviezdy bližšie ku jadru Galaxie sa pohybujú vyššou a hviezdy vzdialenejšie ako Slnko nižšou uhlovou rýchlosťou. Pri pohľade zo Slnka (Zem je v porovnaní so vzdialenosťou hviezd veľmi blízko pri Slnku) sa vlastné pohyby hviezd premietajú do rôznych smerov. V praxi sa vlastné pohyby (ich tangenciálna zložka, radiálne rýchlosti sú určované z posunu spektrálnych čiar objektu) premietajú do rovníkových súradníc: rektascenzie a deklinácie. Ak je ročná hodnota vlastného pohybu μ“ (v oblúkových sekundách), môžeme vyjadriť jej zložky v rektascenzii a deklinácii pomocou tejto hodnoty a pozičného uhla smeru pohybu p:

μ_α^S = (1/15)*μ"*sin p*secδ
μ_δ"*cos p

Pozičný uhol p meriame kladne od severnej časti deklinačnej kružnice smerom k východu. Ak pozeráme na rektascenziu hviezdy vplyvom vlastného pohybu ako na funkciu času, môžeme si vyššie uvedené hodnoty vlastných pohybov predstaviť ako prvú deriváciu tejto funkcie a určením druhej derivácie a pomocou Mc Laurinovho rozvoja (v blízkosti nulového bodu) napísať:

(α_t - α₀)^S = t*μ_α0^S + t²μ_α0^Sμ_α0"*sin1"tanδ₀
(δ_t - δ₀)" = t*μ_δ0 - 0.5*t²(15*μ_α0^S)²*sin1"*sinδ₀*cosδ₀

kde hotnoty t vyjadrujeme v rokoch. Kvadratické členy sa používajú iba výnimočne, pre hviezdy s najväčšími vlastnými pohybmi. Napr. Barnardova hviezda má μ“ = 10,3“ a hviezda ε Ind má μ“ = 4,52“.

6. Redukcie polôh hviezd

V astronomických ročenkách a katalógoch hviezd bývajú udávané stredné polohy hviezd (pre pozorovateľa v strede Slnka) udané strednými súradnicami – vztiahnutými ku strednému pólu a strednému jarnému bodu epochy, teda k rovinám, ktoré (skokom, obvykle po roku) vykonávajú iba precesný pohyb. Ako epocha sa v ročenkách obvykle používa juliánska epocha začiatku kalendárneho roku, odvodeného zo štandardnej epochy J2000.0 po 365,25 dňoch (napr.: polohy J2006,0 alebo prakticky pre výpočty lepšia poloha J2006,5).

Pravá poloha hviezdy je udávaná pravými súradnicami; sú to stredné súradnice voči tým istým rovinám, ktoré sa však v priebehu roka súvisle pohybujú precesiou a nutáciou. Pozorovateľ na Zemi, obiehajúcej okolo Slnka však na oblohe pozoruje zdanlivé polohy, ktoré sú udávané zdanlivými súradnicami, vztiahnutými k pravému pólu a pravému jarnému bodu. Zdanlivé súradnice sú potom získané z pravých súradníc opravou o aberáciu a paralaxu. V prípade vlastného pohybu hviezd musíme túto polohu korigovať aj o túto zložku. Na redukcie môžeme použiť už uvedené sústavy rovníc v predchádzajúcom texte.

7. Objekty v konečnej vzdialenosti

Polohy planét (vrátane Zeme) sú dnes presne vypočítateľné na základe úspešných dynamických teórii pohybu veľkých telies slnečnej sústavy na tisícročia vopred (rovnako i do minulosti). Riešením pohybových rovníc telies v slnečnej sústave (diferenciálnych rovníc II. rádu) sú konštanty integrovania, súvisiace s elementami dráhy. Dve z nich určujú tvar dráhy okolo ťažiska sústavy (pre všetky telesá blízko stredu Slnka): veľká poloos a a výstrednosť e dráhy. Tri ďalšie určujú orientáciu dráhy v rovine ekliptiky: sklon i, dĺžku vzostupného uzla Ω a argument šírky pericentra ω. Posledným elementom je čas prechodu pericentrom T, ktorý definuje polohu telies na dráhe (5).

V praxi sa na výpočet polohy telesa voči Slnku – heliocentrickej – používa systém pravouhlých rovníkových súradníc x, y, z: stred má v strede Slnka, os x mieri do jarného bodu, y je v rovine rovníka 90° od osi x v kladnom smere a os z dopĺňa sústavu do pravotočivej. Ak od týchto súradníc po zložkách odčítame pravouhlé rovníkové súradnice Slnka X, Y, Z (zdanlivé súradnice Slnka pre pozemského pozorovateľa, v časti o paralaxe), dostaneme v rovine rovníka definované pravouhlé geocentrické súradnice telesa voči (hypotetickéhu) geocentrickému pozorovateľovi v strede Zeme. Dôležité je potom tieto geocentrické polohy redukovať na pozorovateľa na povrchu Zeme, v bode s presne definovanými súradnicami λ, φ´ a geocentrickým sprievodičom ρ. Tieto hodnoty závisia od tvaru a veľkosti rotačného dvojosého elipsoidu, ktorým povrch Zeme obvykle aproximujeme; obecne sa v súčasnosti najviac používa sústava WGS 84, ktorá je udávaná pozičným systémom GPS.

Topocentrická korekcia. V meridiánovom reze má Zem tvar elipsy s veľkou poloosou a a malou poloosou b, zviazanými spolu sploštením α (používa sa i výstrednosť elipsy e). Medzi zemepisnou šírkou pozorovateľa φ a geocentrickou šírkou φ´ je iba malý rozdiel, ktorý je najväčší na 45° šírky a možno ho vyjadriť zo vzťahov (4):

α = (a - b)/a
tanφ' = (b²/a²)*tanφ

Druhou súradnicou, definujúcou polohu na povrchu Zeme je geocentrický sprievodič ρ, ktorý možno vyjadriť v jednotkách prijatého rovníkového polomeru elipsoidu a v presnom tvare:

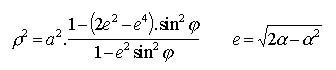
alebo v niektorom z približných tvarov vo forme konvergujúceho radu, ktoré obsahujú učebnice vyššej geodézie. Reálny tvar Zeme (geoid) sa zhoduje s matematicky definovanou plochou iba približne (+50 m Koralové more a až -100 m indický subkontinent) a pri extrémnych nadmorských výškach treba pridať ďalšie korekcie. Tretia sférická súradnica – zemepisná dĺžka – sa nemení. Ak vyjadríme polohu pozorovateľa v čase pozorovania v pravouhlých geocentrických súradniciach (orientovaných zhodne s heliocentrickými), dostaneme topocentrické polohy telies na oblohe ich odčítaním od geocentrických. Nakoniec zostáva riešiť iba sústavu súradníc (po zložkách):

x = ρ*cosα*cosδ
y = ρ*sinα*cosδ
z = ρ*sinδ

z ktorej určíme okrem vzdialenosti ρ (ako odmocninu zo súčtu druhých mocnín zložiek x, y, z) aj topocentrické hodnoty rektascenzie a deklinácie.

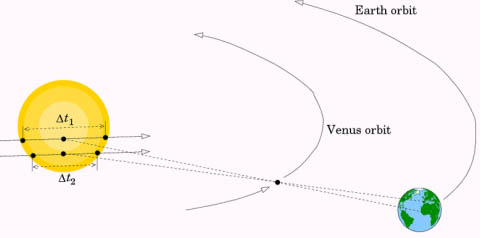
Obr.3. Pre každého pozorovateľa na Zemi trvá prechod Venuše pred slnečným diskom rôzne dlho. Metódu, ako z najmenej hodnoty dvoch rôznych pozorovaní tohto javu určiť paralaxu Slnka, navrhol už v r. 1705 Edmund Halley.

Analogicky ročnej paralaxe hviezd môžeme pre telesá v konečnej vzdialenosti zaviesť pre pozemského – topocentrického – pozorovateľa horizontálnu paralaxu. Horizontálnu preto, lebo posúva nebeské telesá (v porovnaní s geocentrickou polohou) k horizontu pozorovateľa. Jej hodnota závisí od vzdialenosti pozorovateľa a daného telesa; uhlovo je to veľkosť priemetu vzdialenosti stredu Zeme a pozorovateľa z pozorovaného telesa do hlavnej kružnice na oblohe, ktorá obe tieto polohy spája. Tento posun je najväčší pri východe a západe telesa a minimálny v kulminácii. Pre telesá v zenite je horizontálna paralaxa nulová.

Obr.4: Na kompozícii P. Lawrenceho vidíme polohu Mesiaca medzi hviezdami pre dvoch pozorovateľov vzdialených 5220 km pri súčasnom fotografovaní pri zatmení 28. 10. 2004. Mesiac je najbližším prirodzeným telesom a jeho stredná horizontálna paralaxa je 3422,6“. Pod týmto uhlom by sme videli rovníkový polomer Zeme zo strednej vzdialenosti Mesiaca od Zeme zo stredu Mesiaca.

Pri pozorovaniach blízkych objektov musíme zobrať do úvahy i konečnú rýchlosť, ktorou sa šíri z telesa odrazené slnečné svetlo. Ak pozorujeme napr. asteroid vo vzdialenosti 1 AU, vidíme jeho polohu nie v čase pozorovania, ale v čase o 499 sekúnd skôr. Najmä pri určovaní dráh týchto telies z polôh musíme postupnými aproximáciami zaviesť aberačný čas – korekciu času pozorovaní na vzdialenosti telesa (napríklad Slnko sa za 499 sekúnd posunie voči hviezdam priemerne o 20,5“).

8. Ako presne počítať?

V praxi vždy vychádzame z našej praktickej potreby a možností, iba tak sa vyhneme dlhotrvajúcim a možno zbytočným výpočtom. Základom je presnosť určenia polohy a presnosť merania času. Rádiom riadené hodiny spolu so stopkami a zručným pozorovateľom neumožnia dostať sa v časovej presnosti pod 0,3 sekundy. Premietnuté do uhlových rozmerov tento čas zodpovedá pri rýchlosti otáčania Zeme uhlovú nepresnosť okolo 4,5“. Podobne presne by sme mali poznať svoju polohu; 1“ v smere severo-južnom je u nás asi 30,5 metra, v smere kolmom asi 21 metrov. Rovnako presne musí byť nastavená montáž ďalekohľadu: najmä polárna os. Z našej vlastnej praxe, keď môžeme delené kruhy nášho ďalekohľadu nastavovať pomocou nónia na 5 sekúnd v hodinovom uhle (75“) a 0,5´ v deklinácii (30“) vidíme, že takáto presnosť je predimenzovaná. S rozlíšením okolo 1´ sme skôr v „sextatnovej“ sieti; námorná míľa je 1853 metrov a 1´ na poludníku.... Teória je však neúprosná a vyžaduje o rád lepšie rozlíšenie, ako prax. V nej by sme určite počítali s refrakciou, aberáciou, precesiou a horizontálnou paralaxou.

Presnejšie sa do času dostaneme používaním dnes už štandardných vkladačov času (na báze DCF 77 alebo GPS) do objektívneho (najmä video-) záznamu. Rozlíšenie 0,04 časovej sekundy uhlovo predstavuje 0,6“, čo zasa vyžaduje zmerať polohu pomocou GPS prístroja s diferanciálnymi opravami. Ku štandardným vplyvom refrakcie, horizontálnej paralaxy, aberácie a precesie by sme museli pridať aj nutáciu a u niektorých hviezd i vlastné pohyby. Vyspelé softvéry majú možnosť „prepínať“ pri zobrazení polôh objektov na oblohe medzi pravými, strednými a zdanlivými polohami. Rovnako používajú opravy v aberačnom čase a u telies blízkych rozlišujú geocentrické a topocentrické polohy.

Pre blízke telesá je v súčasnosti najpoužívanejším postupom je vyhľadať efemeridu na web interface JPL: http://ssd.jpl.nasa.gov/horizons.cgi, kde je možné zadať všetky možné (i nemožné) detaily a kde sú vo výslednom produkte aj bohaté vysvetlenia ku použitej súradnicovej sústave.

(1) Horský Z., Kalivoda J.: Hvězdy, hvězdáři a hvězdopravci, prémie Antické knihovny, Svoboda Praha, 1986
(2) Uhlig.L., Steinfatt.W.: Astronomische Navigation, Verlag fur Werkehrwesen, 3. vydanie Berlin, 1979
(3) Pittich E. – editor.: Astronomická ročenka 2006, SUH Hurbanovo, 2005
(4) Procházka J.: Geodetická astronomie, VAAZ Brno, 1966
(5) Dubošin D.N. – editor: Spravočnoje rukovodstvo po nebesnoj mechanike i astrodinamike, Nauka, Moskva 1976